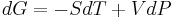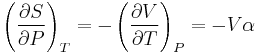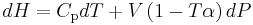Joule–Thomson effect
- Throttling process redirects here. For the regulation of computing resources, see throttling process (computing).
In thermodynamics, the Joule–Thomson effect or Joule–Kelvin effect or Kelvin–Joule effect describes the temperature change of a gas or liquid when it is forced through a valve or porous plug while kept insulated so that no heat is exchanged with the environment.[1][2][3] This procedure is called a throttling process or Joule–Thomson process.[4] At room temperature, all gases except hydrogen, helium and neon cool upon expansion by the Joule–Thomson process.[5][6]
The effect is named for James Prescott Joule and William Thomson, 1st Baron Kelvin who discovered it in 1852 following earlier work by Joule on Joule expansion, in which a gas undergoes free expansion in a vacuum.
Contents |
Description
The adiabatic (no heat exchanged) expansion of a gas may be carried out in a number of ways. The change in temperature experienced by the gas during expansion depends not only on the initial and final pressure, but also on the manner in which the expansion is carried out.
- If the expansion process is reversible, meaning that the gas is in thermodynamic equilibrium at all times, it is called an isentropic expansion. In this scenario, the gas does positive work during the expansion, and its temperature decreases.
- In a free expansion, on the other hand, the gas does no work and absorbs no heat, so the internal energy is conserved. Expanded in this manner, the temperature of an ideal gas would remain constant, but the temperature of a real gas may either increase or decrease, depending on the initial temperature and pressure.
- The method of expansion discussed in this article, in which a gas or liquid at pressure P1 flows into a region of lower pressure P2 via a valve or porous plug under steady state conditions and without change in kinetic energy, is called the Joule–Thomson process. During this process, enthalpy remains unchanged (see a proof below).
A throttling process proceeds along a constant-enthalpy line in the direction of decreasing pressure, which means that the process occurs from left to right on a T-P diagram. As we proceed along a constant-enthalpy line from high enough pressures the temperature increases, until the inversion temperature. After this, as the fluid continues its expansion, the temperature drops. If we do this for several constant enthalpies and join the inversion points a line called the inversion line is obtained. This line intersects the T-axis at some temperature, named the maximum inversion temperature. For hydrogen this temperature is -68°. In Vapour-compression refrigeration we need to throttle the gas and cool it at the same time. This poses a problem for substances whose maximum inversion temperature is well below room temperature. Thus hydrogen must be cooled below its inversion temperature if any cooling is achieved by throttling.[7]
Physical mechanism
As a gas expands, the average distance between molecules grows. Because of intermolecular attractive forces (see Van der Waals force), expansion causes an increase in the potential energy of the gas. If no external work is extracted in the process and no heat is transferred, the total energy of the gas remains the same because of the conservation of energy. The increase in potential energy thus implies a decrease in kinetic energy and therefore in temperature.
A second mechanism has the opposite effect. During gas molecule collisions, kinetic energy is temporarily converted into potential energy. As the average intermolecular distance increases, there is a drop in the number of collisions per time unit, which causes a decrease in average potential energy. Again, total energy is conserved, so this leads to an increase in kinetic energy (temperature). Below the Joule–Thomson inversion temperature, the former effect (work done internally against intermolecular attractive forces) dominates, and free expansion causes a decrease in temperature. Above the inversion temperature, gas molecules move faster and so collide more often, and the latter effect (reduced collisions causing a decrease in the average potential energy) dominates: Joule–Thomson expansion causes a temperature increase.
The Joule–Thomson (Kelvin) coefficient
The rate of change of temperature  with respect to pressure
with respect to pressure  in a Joule–Thomson process (that is, at constant enthalpy
in a Joule–Thomson process (that is, at constant enthalpy  ) is the Joule–Thomson (Kelvin) coefficient
) is the Joule–Thomson (Kelvin) coefficient 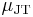 . This coefficient can be expressed in terms of the gas's volume
. This coefficient can be expressed in terms of the gas's volume  , its heat capacity at constant pressure
, its heat capacity at constant pressure 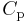 , and its coefficient of thermal expansion
, and its coefficient of thermal expansion  as:[1][3][8]
as:[1][3][8]
See the Derivation of the Joule–Thomson (Kelvin) coefficient below for the proof of this relation. The value of 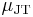 is typically expressed in °C/bar (SI units: K/Pa) and depends on the type of gas and on the temperature and pressure of the gas before expansion. Its pressure dependence is usually only a few percent for pressures up to 100 bar.
is typically expressed in °C/bar (SI units: K/Pa) and depends on the type of gas and on the temperature and pressure of the gas before expansion. Its pressure dependence is usually only a few percent for pressures up to 100 bar.
All real gases have an inversion point at which the value of 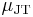 changes sign. The temperature of this point, the Joule–Thomson inversion temperature, depends on the pressure of the gas before expansion.
changes sign. The temperature of this point, the Joule–Thomson inversion temperature, depends on the pressure of the gas before expansion.
In a gas expansion the pressure decreases, so the sign of 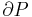 is negative by definition. With that in mind, the following table explains when the Joule–Thomson effect cools or warms a real gas:
is negative by definition. With that in mind, the following table explains when the Joule–Thomson effect cools or warms a real gas:
| If the gas temperature is | then 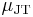 is is |
since 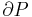 is is |
thus 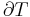 must be must be |
so the gas |
|---|---|---|---|---|
| below the inversion temperature | positive | always negative | negative | cools |
| above the inversion temperature | negative | always negative | positive | warms |
Helium and hydrogen are two gases whose Joule–Thomson inversion temperatures at a pressure of one atmosphere are very low (e.g., about 51 K (−222 °C) for helium). Thus, helium and hydrogen warm up when expanded at constant enthalpy at typical room temperatures. On the other hand nitrogen and oxygen, the two most abundant gases in air, have inversion temperatures of 621 K (348 °C) and 764 K (491 °C) respectively: these gases can be cooled from room temperature by the Joule–Thomson effect.[1]
For an ideal gas, 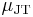 is always equal to zero: ideal gases neither warm nor cool upon being expanded at constant enthalpy.
is always equal to zero: ideal gases neither warm nor cool upon being expanded at constant enthalpy.
Applications
In practice, the Joule–Thomson effect is achieved by allowing the gas to expand through a throttling device (usually a valve) which must be very well insulated to prevent any heat transfer to or from the gas. No external work is extracted from the gas during the expansion (the gas must not be expanded through a turbine, for example).
The effect is applied in the Linde technique as a standard process in the petrochemical industry, where the cooling effect is used to liquefy gases, and also in many cryogenic applications (e.g. for the production of liquid oxygen, nitrogen, and argon). Only when the Joule–Thomson coefficient for the given gas at the given temperature is greater than zero can the gas be liquefied at that temperature by the Linde cycle. In other words, a gas must be below its inversion temperature to be liquefied by the Linde cycle. For this reason, simple Linde cycle liquefiers cannot normally be used to liquefy helium, hydrogen, or neon.
Proof that enthalpy remains constant in a Joule–Thomson process
In a Joule–Thomson process the enthalpy remains constant. To prove this, the first step is to compute the net work done by the gas that moves through the plug. Suppose that the gas has a volume of V1 in the region at pressure P1 (region 1) and a volume of V2 when it appears in the region at pressure P2 (region 2). Then the work done on the gas by the rest of the gas in region 1 is P1V1. In region 2 the amount of work done by the gas is P2V2. So, the total work done by the gas is
The change in internal energy plus the work done by the gas is, by the first law of thermodynamics, the total amount of heat absorbed by the gas (here it is assumed that there is no change in kinetic energy). In the Joule–Thomson process the gas is kept insulated, so no heat is absorbed. This means that
where 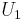 and
and 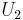 denote the internal energy of the gas in regions 1 and 2, respectively.
denote the internal energy of the gas in regions 1 and 2, respectively.
Using the definition of enthalpy 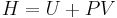 , the above equation then implies that:
, the above equation then implies that:
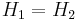
where 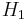 and
and 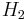 denote the enthalpy of the gas in regions 1 and 2, respectively.
denote the enthalpy of the gas in regions 1 and 2, respectively.
Derivation of the Joule–Thomson (Kelvin) coefficient
A derivation of the formula
for the Joule–Thomson (Kelvin) coefficient.
The partial derivative of T with respect to P at constant H can be computed by expressing the differential of the enthalpy dH in terms of dT and dP, and equating the resulting expression to zero and solving for the ratio of dT and dP.
It follows from the fundamental thermodynamic relation that the differential of the enthalpy is given by:
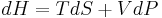 (here,
(here,  is the entropy of the gas).
is the entropy of the gas).
Expressing dS in terms of dT and dP gives:
Using
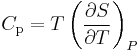 (see Specific heat capacity), we can write:
(see Specific heat capacity), we can write:
The remaining partial derivative of S can be expressed in terms of the coefficient of thermal expansion via a Maxwell relation as follows. From the fundamental thermodynamic relation, it follows that the differential of the Gibbs energy is given by:
The symmetry of partial derivatives of G with respect to T and P implies that:
where  is the coefficient of thermal expansion. Using this relation, the differential of H can be expressed as
is the coefficient of thermal expansion. Using this relation, the differential of H can be expressed as
Equating dH to zero and solving for dT/dP then gives:
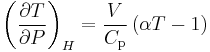
It is easy to verify that for an ideal gas the thermal expansion coefficient  is
is  , and so an ideal gas does not experience a Joule–Thomson effect. The cooling of a gas by pure isentropic expansion is not Joule-Thomson cooling, although it is sometimes erroneously called J-T cooling by some laboratory practitioners.
, and so an ideal gas does not experience a Joule–Thomson effect. The cooling of a gas by pure isentropic expansion is not Joule-Thomson cooling, although it is sometimes erroneously called J-T cooling by some laboratory practitioners.
See also
- Critical temperature
- Ideal gas
- Enthalpy and Isenthalpic
- Refrigeration
- Reversible process (thermodynamics)
References
- ^ a b c R. H. Perry and D. W. Green (1984). Perry's Chemical Engineers' Handbook. McGraw-Hill. ISBN 0-07-049479-7.
- ^ B. N. Roy (2002). Fundamentals of Classical and Statistical Thermodynamics. John Wiley & Sons. ISBN 0-470-84313-6.
- ^ a b W. C. Edmister, B. I. Lee (1984). Applied Hydrocarbon Thermodynamics. Vol. 1 (2nd ed.). Gulf Publishing. ISBN 0-87201-855-5.
- ^ F. Reif (1965). "Chapter 5 – Simple applications of macroscopic thermodynamics". Fundamentals of Statistical and Thermal Physics. McGraw-Hill. ISBN 0070518009.
- ^ A. W. Adamson (1973). "Chapter 4 – Chemical thermodynamics. The First Law of Thermodynamics". A textbook of Physical Chemistry (1st ed.). Academic press. LCCN 720328.
- ^ G. W. Castellan (1971). "Chapter 7 – Energy and the First Law of Thermodynamics; Thermochemistry". Physical Chemistry (2nd ed.). Addison-Wesley. ISBN 0201009129.
- ^ Thermodynamics An Engineering Approach (6th ed.). McGraw Hills. 2007.
- ^ W.R. Salzman. "Joule Expansion". Department of Chemistry, University of Arizona. http://www.chem.arizona.edu/~salzmanr/480a/480ants/jadjte/jadjte.html.
Bibliography
- M. W. Zemansky (1968). Heat and Thermodynamics; An Intermediate Textbook. McGraw-Hill. pp. 182, 355. LCCN 670891.
- D. V. Schroeder (2000). An Introduction to Thermal Physics. Addison Wesley Longman. p. 142. ISBN 0-201-38027-7.
- C. Kittel, H. Kroemer (1980). Thermal Physics. W. H. Freeman. ISBN 0-7167-1088-9.
External links
- "Joule–Thomson process". Eric Weisstein's World of Physics. http://scienceworld.wolfram.com/physics/Joule-ThomsonProcess.html.
- "Joule–Thomson coefficient". Eric Weisstein's World of Physics. http://scienceworld.wolfram.com/physics/Joule-ThomsonCoefficient.html.
- "Joule–Thomson effectt". the truncated free online version of the Encyclopædia Britannica. http://www.britannica.com/eb/article?tocId=9044025&query=Joule-Thomson%20effect&ct=.
- "Inversion Curve of Joule-Thomson Effect using Peng-Robinson CEOS". Demonstrations Projects of Wolfram Mathematica. http://demonstrations.wolfram.com/InversionCurveOfJouleThomsonUsingThePengRobinsonCubicEquatio/.
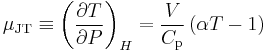
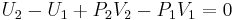
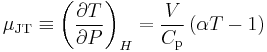
![dH = T\left(\frac{\partial S}{\partial T}\right)_{P}dT %2B \left[V%2BT\left(\frac{\partial S}{\partial P}\right)_{T}\right] dP\,](/2012-wikipedia_en_all_nopic_01_2012/I/f234d553439e0fbad1436f6e5d9cc886.png)
![dH = C_{\mathrm{p}}dT %2B \left[V%2BT\left(\frac{\partial S}{\partial P}\right)_{T}\right] dP\,](/2012-wikipedia_en_all_nopic_01_2012/I/6e1259b2941be4e6aaa17d19afc874ff.png)